理論模型方法
相平衡的實驗數據包括壓力、溫度和組成。同樣,對相平衡的理論研究也是論述系統處于平衡態時系統的壓力、溫度、各相的體積及組成關系,更進一步,還要根據熱力學函數關系進行相互推算。
實驗得到的汽液相平衡數據只是一些離散的點,最開始只是用作圖的方法連接這些實驗點,再采用內插法獲得更多的實踐所需要的數據。這種內插或者外推得到的值可能產生較大偏差,因此可靠的數據處理方法是依據熱力學基本原理將實驗數據轉換成溫度、壓力、組成的函數。根據相平衡原理,除溫度和壓力外,每組分在各項中的化學位必須相等,則平衡條件可表示為:
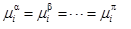
式中μi表示組分i的化學位,上標α,β,…π表示不同的相。
根據逸度的定義,平衡條件也可表示為:
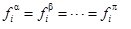
式中fi表示組分i的逸度。此是解決相平衡關系的最基本公式。這里的唯一問題是我們如何將逸度與體系的溫度、壓力和組成關聯起來。
對于汽液相平衡,相平衡判據式可寫為:
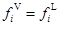 (1)
(1)
式中V代表汽相,L代表液相,式中fiV、fiL分別表示汽相、液相組分i的逸度。該式是汽液平衡計算的最基本公式。由逸度、逸度系數和活度、活度系數的定義,組分i的逸度可由逸度系數或活度系數表示。對于氣相則有,
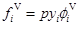
φiV為汽相中組分i的逸度系數,對于液相則有:
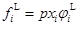 (3a)
(3a)
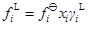
fi?為組分i在標準狀態下的逸度,取Lewis-Randall定律為基準的標準態;γiL為組分i的液相活度系數;φiL為組分i的液相逸度系數。由于液相的逸度有(3a)、(3b)兩種表達方式,所以,常用的汽液相平衡計算式可根據液相逸度表示方法的不同而分為:活度系數法(γi)和狀態方程法(Equation of State, EoS)兩種。
狀態方程法(EoS)
液相逸度以(3a)式表示時,則根據式(1)、(2)和(3a)可得到:
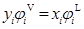 (4)
(4)
式中φiV、φiL需要利用合適的狀態方程來計算,狀態方程法來計算汽液相平衡關鍵是能找到汽液兩相都適合的狀態方程以及相應的混合規則,并根據狀態方程導出φiV、φiL的表達式。利用這種方法不用計算活度,所以不用選擇標準態,滿足熱力學一致性原理。到目前為止,有關狀態方程的報道很多,開發的狀態方程種類繁多,如Vander Waals狀態方程、維里方程、立方型方程(SRK、PR等)、鏈流體狀態方程等等。
活度系數法
液相逸度采用(3b)式表示時,根據和(1)、(2)、(3b)可得到:
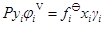 (5)
(5)
取以Lewis-Randall規則為基準的標準態,則標準態的逸度是平衡溫度、壓力下純組分i的逸度,則有:
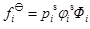 (6a)
(6a)
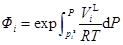 (6b)
(6b)
式中Фi被稱為Poynting因子,表示壓力對標準態液相逸度的校正,pis為純組分i在溫度T下的飽和蒸汽壓,φis是純組分i在溫度T和pis下的逸度系數,ViL是純組分i在溫度T時液相的摩爾體積。聯合式(5)、(6a)、(6b)可以得到:
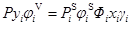 (7)
(7)
式(7)根據系統壓力的不同可以進行簡化,在壓力處于中低壓的情況下,對于非極性或者微極性混合物,汽相可視為理想氣體,則有φiV=1且φis=1,此時Poynting因子Фi≈1,則(7)式可以簡化為:
 (8)
(8)
式中pis與溫度的關系可用Antoine方程(9)來表示,根據實驗測得的平衡溫度可以計算出pis的值。
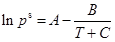
而活度系數γi的計算可選擇合理的活度系數模型來進行計算。活度系數模型發展至今,大致分為兩類:一類是以Van Laar式、Margules式和溶解度參數式為代表的模型,其是在正規溶液理論基礎上發展起來的模型,這類活度系數模型對于簡單系統能獲得較為理想的結果;另一類是上世紀60年代以后以Wilson、NRTL、UNIQUAC模型為代表,在似晶格理論基礎上,引入局部組成概念發展形成。這類模型參數較少,能利用較少的實驗數據關聯出模型參數并推算混合物性質。
近年來還基于量子化學計算發展起了先驗性的預測模型——COSMO,目前主要有兩種,即COSMO-RS和COSMO-SAC,該類模型的預測結果只依賴于量子計算的分子構型和表面電荷密度分布。
活度系數法和狀態方程法的比較

